Simple exam-score curving with MTM

We’ve all done it. You set what seems to be a reasonable exam but then the average comes out to be an F grade and all the students start freaking out. The immediate call is to curve the scores up! I think this is generally a good idea, because students are conditioned to expect an average score around 70% to 80% for exams and they will be stressed if it is much below this. But now the question arises: “How exactly should we curve the scores?” Here I’ll show the super-simple MTM method that works well in practice.

The MTM curving function

The MTM (Median-To-Median) method scales an old exam score S₀ to a new exam score S₁ by:

• S₁ = 100 − (100 − S₀) × (100 − M₁) / (100 − M₀), if S₀ > M₀
• S₁ = S₀ + M₁ − M₀, if S₀ ≤ M₀

In these equations, M₀ is the median of the old score distribution, which should be computed from the set of all old scores. We assume scores are in the range 0 to 100. There is just one parameter that needs to be chosen:

• M₁ = the new median score (80 is a good choice for this).

Here is an Excel file that implements this curving function:

As an example, if the old median was M₀ = 60 and we choose a new median of M₁ = 80 then the MTM curving function is:

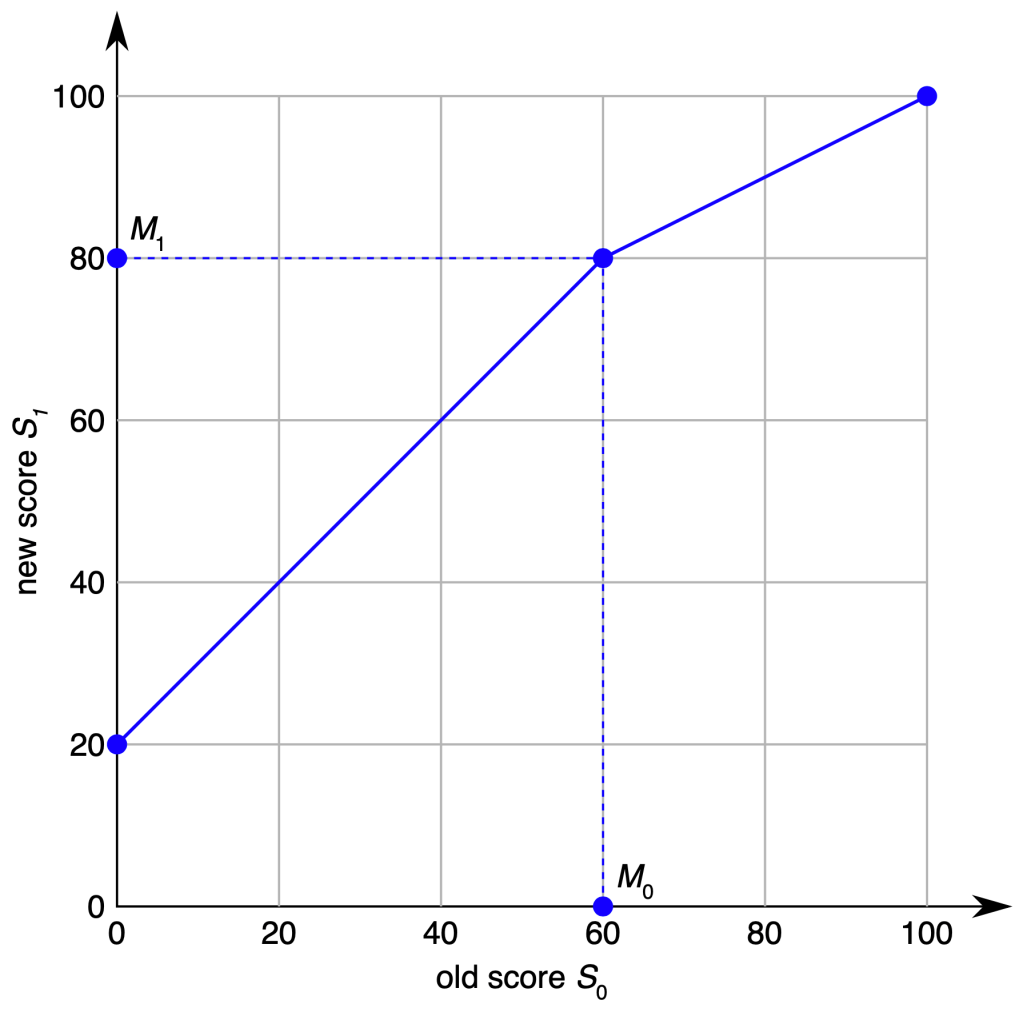
As we can see, the MTM curving function is piecewise linear with a slope of 1 below the old median and it connects the point (M₀,M₁) to (100,100) above the old median.

Why is MTM a good curving function?

The advantages of MTM as a curving function are:

1. It’s simple to implement.
2. Assuming that the new median is higher than the old median, it’s guaranteed that every student’s score increases, but cannot go over 100, and the ordering between scores is strictly maintained.
3. A perfect score of 100 maps to 100.
4. Using the median as the specification point makes MTM insensitive to outliers. We generally want M₁ ≈ 80, putting half the class in the A/B range (more when high-scoring items like homeworks are included).
5. All below-median students get the same score boost, which is simple and fair.

Of course it’s possible to use more complex piecewise linear functions to give more fine-grained control over the score distribution. This might sometimes be needed, but I’ve found that in practice using MTM with just a single parameter (the new median score) is sufficient and much easier to choose.

Extension: two-parameter MTM

While the MTM function above is sufficient in almost all situations, sometimes it’s helpful to give an even higher boost to low-scoring students. In this case we can add an extra parameter:

• Z = the extra boost given to a student who scored zero on the original test.

The curving function is then extended to the 2-parameter MTM:

• S₁ = 100 – (100 – S₀) × (100 – M₁) / (100 – M₀), if S₀ > M₀
• S₁ = S₀ + M₁ − M₀ + (1 − S₀/M₀) × Z, if S₀ ≤ M₀

This function has all the same properties as the original MTM, except that the lowest-scoring students get an even higher boost (so long as Z is more than zero).